图形学概念介绍

计算机图形学主要分为光栅化（openGL）曲线曲面（几何）光线追踪动画与模拟

光栅化：简而言之就是将三维空间的几何形体显示在屏幕上
实时生成指的是每秒钟至少生成30张画面否则就叫离线
曲线曲面：如何生成光滑的曲线曲面，如何用简单曲面生成复杂曲面，如何保持物体的拓扑结构
光线追踪：生成真实的画面

向量

图形学中的向量默认是列向量，转置是行向量

2D
$\vec{a}\cdot\vec{b}=\begin{pmatrix}x_a\\y_a\end{pmatrix}\cdot\begin{pmatrix}x_b\\y_b\end{pmatrix}=x_ax_b+y_ay_b$
3D
$\vec a\cdot\vec b=\begin{pmatrix}x_a\\y_a\\z_a\end{pmatrix}\cdot\begin{pmatrix}x_b\\y_b\\z_b\end{pmatrix}=x_ax_b+y_ay_b+z_az_b$

向量b在a上的投影： $(||b||cos\theta) ∗ a$

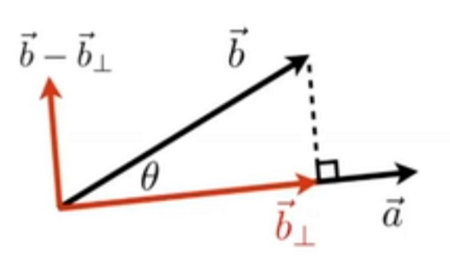
向量 $a \times b$ 也就是叉乘的结果 $c$ 是一个同时垂直于 $a$ 和 $b$ 的向量常用于求法线
$\vec{a}\times\vec{b}=\begin{pmatrix}y_az_b-y_bz_a\\z_ax_b-x_az_b\\x_ay_b-y_ax_b\end{pmatrix}$

$c$ 的方向可以用右手螺旋定则得到（右手坐标系下）
四指从 $a$ 转到 $b$ 大拇指方向就是 $c$ 的方向

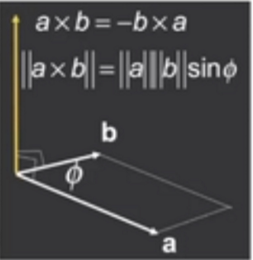
应用： axb 叉乘结果为正则说明在b在a的左侧为负在右侧

接着进一步就可以判断点在图形内部还是外部了

即分别计算ABxAP BCxBP CAxCP 若叉乘结果都为同号则说明该点同时在这三个向量同侧
也就说明在图形内部

注意是哪三个向量反着来也行但是都要按顺序

矩阵

矩阵相乘: $AxB = C$
其中 $C[i][j]$ 就等于 $A$ 的第 $i$ 行与 $B$ 的第 $j$ 列逐项相乘求和的结果

矩阵乘法没有交换律

求一个二维向量关于y轴的对称左乘一个矩阵即可
$\begin{pmatrix}-1&0\\0&1\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}-x\\y\end{pmatrix}$

$(AB)$ 的转置等于 $B$ 的转置乘 $A$ 的转置
即 $(AB)^T=B^TA^T$

矩阵的逆也是同理
即 $(AB)^{-1} = B^{-1}A^{-1}$

向量的点乘和叉乘都可以表示成矩阵形式
$\vec a\cdot\vec b=\vec a^T\vec b\\=\begin{pmatrix}x_a&y_a&z_a\end{pmatrix}\begin{pmatrix}x_b\\y_b\\z_b\end{pmatrix}\\=\begin{pmatrix}x_ax_b+y_ay_b+z_az_b\end{pmatrix}$

$\vec{a}\times\vec{b}=A^*b=\begin{pmatrix}0&-z_a&y_a\\z_a&0&-x_a\\-y_a&x_a&0\end{pmatrix}\begin{pmatrix}x_b\\y_b\\z_b\end{pmatrix}$

齐次坐标的意义在于为了将平移坐标纳入统一的变换矩阵中
一般用（x，y，1）表示点的齐次坐标，（x，y，0）表示向量的齐次坐标

光栅化

谈到光栅化（Rasterization）我们就不得不提一下实时渲染的核心组件——图形渲染管线（The Graphics Rendering Pipeline），它的主要功能是在给定一个虚拟相机、三维物体、光源等等的情况下生成或渲染二维图像（如下图）。

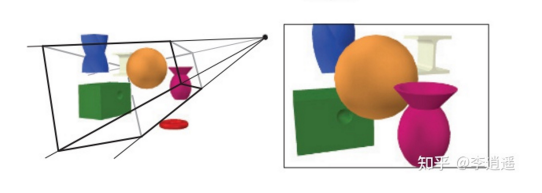
实时渲染管线（Real-Time Rendering Pipeline）的各阶段是并行执行的，每个阶段都取决于上一阶段的结果。大致分为四个主要阶段：

应用程序阶段（Application）
几何处理阶段（Geometry Processing）
光栅化阶段（Rasterization）
像素处理阶段（Pixel Processing）

屏幕映射（视口变换）：对于标准立方体[-1, 1]³，先不管它的Z轴数据（由深度缓冲来处理），屏幕映射需要将X和Y轴 [-1, 1]² 映射到屏幕坐标 [0, width] x [0, height]，和MVP变换类似，通过齐次坐标的矩阵，先将 [-1, 1]² 缩放至 [width, height]

因为标准立方体中心在原点，而屏幕原点在左下角，所以还需要经过一个平移使得原点坐标对齐，将标准立方体转换成屏幕空间，变为窗口坐标系，变换矩阵为：
$M_{viewport}=\begin{bmatrix}\dfrac{width}{2}&0&0&\dfrac{width}{2}\\0&\dfrac{height}{2}&0&\dfrac{height}{2}\\0&0&1&0\\0&0&0&1\end{bmatrix}$

如何进行光栅化

先做一个视口变换，映射到屏幕空间，到这一步的时候大家不要忘了我们此时得到的不过是屏幕空间中的一些三角而已，但是这远远不够。

我们需要把这些三角形打碎打成像素并且告诉每个像素的值是多少然后显示在屏幕上。因此利用
像素的中心对屏幕空间进行采样，遍历全部三角形中的像素，然后判断像素的中心点是否在三角形内部，如果在就赋值为1并显示。

这样我们就会发现一个问题，我们想要得到的是一个三角形，但是实际得到的不完完全是一个三角形，不过的它的形状和三角形大概类似，这就是我们所说的锯齿（或者说走样）。

有两个原因导致锯齿：

一是像素本身有一定的大小
二是采样的速度更不上信号变化的速度（高频信号采样不足）。

采样所产生的瑕疵

锯齿
摩尔纹
车轮错觉

如何进行反走样呢

可以在采样之前先做模糊再采样（模糊也可以认为是低通滤波器，把三角形边界的这种高频信号给过滤掉）。

为什么模糊（预过滤）然后采样可以进行抗锯齿？

模糊（Blurring/Pre-Filtering ）就是要剔除某些特定频率的内容。模糊是通过低通滤泼器把高频信号剔除从而不会产生信号混叠，从而来解决反走样的问题。

人们研究出一种近似算法也就是所谓的超采样MSAA, MSAA只是一个反走样的近似，并不能严格的解决反走样的问题。

MSAA的算法是将一个像素划分成许多个小像素，每个小像素都有一个中心，算面积覆盖率就是可以等同于有几个采样点在这个三角形，如果像素点足够多的话就可以取得比较好的结果。

为什么经过一系列的空间变换和视口变换得到的是一系列屏幕空间的三角形？

这是因为三角形在图形学中可以看做是几何体的基本形状（Triangles - Fundamental Shape Primitives）

那可能又有人会想为什么是三角形呢？

因为三角形在图形学中有很多很好的性质：

三角形是最基本的多边形，并且任何其他的多边形都可以拆分为三角形。
三个点可以保证他在一个平面, 如果是四边形四个点就不能保证。
它可以很好地用叉积判断一个点是不是在三角形内部（三角形的内外定义特别清晰）

光线追踪

光线追踪（Ray Tracing）算法是一种计算机三维图形渲染算法，其基本出发点就是追踪光线，模拟真实的光路和成像过程。

相比于其他大部分渲染算法，光线追踪算法的优势是可以提供更为真实的光影效果，劣势是计算量巨大。

算法原理

从视点出发向屏幕上每一个像素发出一条光线，追踪此光路并计算其逆向光线的方向，映射到对应的像素上。如下图，通过计算光路上颜色衰减和叠加，即可基本确定每一个像素的颜色。

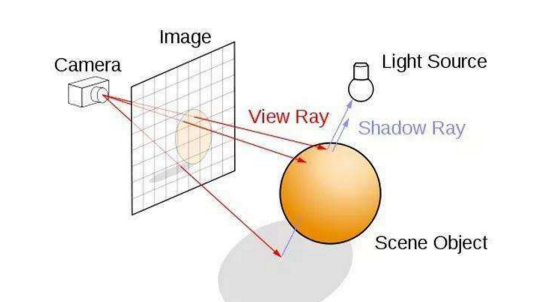
主要包括相交检测、计算光线反射和折射。

对反射和折射后的光线递归计算颜色再叠加起来即可算得原光线颜色。若光线未遇到任何物体则返回背景色。

相交检测

大多数情况下，场景中的三维物体是由众多三角形面片组合而成的，可以视为场景中实际上有一大堆三角面片，判断光线是否与场景中的物体碰撞，实际上是计算光线与三角形相交，找出离眼睛最近的那个相交的三角形。

用最土的方法就是访问每一个三角形面片，计算光线是否跟它相交，现代的方法就是借助空间上的加速结构(例如BVH和KD树)，快速找到相交的三角形。

经典光线追踪

经典光线追踪，光线会计算击中物体后的反射方向(很少用到折射)，通常计算的是镜面反射，得到反射方向后，光线不会继续朝新方向前进(经典光线追踪最重要的特征之一)，意味着光线发生首次碰撞后便会就此打住，不会继续前进。

那么计算的反射方向是用来干嘛用呢？其实用来计算像素颜色值的，不是用来作为新的前进方向的。

光线首次击中物体，那么就能得到碰撞点，然后将该点与光源连一条线(简单的是用点光源)，判断这条线能不能直达光源，也就是计算这条线有没有与其他物体发生相交，如果有相交，则说明光源射到碰撞点的光被遮挡了，那么就按照渲染方程去计算阴影下这个像素点的颜色值；如果没有发生相交，则说明光源能直接照射到碰撞点，那就计算光照下的像素点颜色。

之前计算得到的光线反射方向，用来计算光源与碰撞点之间的连线在反射方向上的投影(利用向量点乘计算)，理解为光源对这条光线的贡献值。

递归式光线追踪

光线在场景中会发生多次碰撞，这一点正是递归光线追踪和经典光线追踪的区别处。

同样是从人眼出发发射光线，穿过屏幕进入场景中，寻找光线最近的碰撞点，这开头都和经典光线追踪一模一样。关键在找到光线的首次碰撞点后，经典光线追踪是直接利用这个点和光源一起计算像素颜色值。而递归光线追踪则是将这个碰撞点作为光线的新起点，再在这个点上计算光线的反射方向作为光线的新方向，然后继续追踪这条光线，即继续寻找这条新光线的最近碰撞点(从算法实现上，这一步可以用递归函数去实现)。

接下来，光线遇到新的碰撞点，就生成新的反射光线继续追踪，连起来看就是一条光路，而我们就是在追踪这条光路，那么这条光路最终的结局无非就是两种：

光线命中光源（这时光源可以是面光源、点光源，为了提高命中率，通常选面光源），利用这条光线沿途得到的信息来计算相应像素点的颜色值，沿途的信息是指中途的碰撞点（可以知道这个碰撞点是在哪个球上，这个球是什么颜色的等等），将各个碰撞点上的信息套入渲染方程计算，其实就是将各个碰撞点对光线做出的贡献进行混合。
例如上图中A1是红色的，A2是蓝色的，A3是绿色的，光线每碰撞一次都会乘一个衰减系数（如0.8），用来减弱后续碰撞点贡献的权重，将各个点的颜色等信息带上衰减系数一起套入渲染方程里搅浑、混合、整合一下，结果值就是我们眼睛接受到这条光线的贡献值，即相应像素点的颜色值。（从结果上看，我们现在就能从玻璃球的表面看到反射的其他玻璃球了，因为像素颜色中有其他玻璃球上碰撞点的贡献）
第二个结局就是光线没有命中光线，就是光线最后没有与任何三角形面片发生相交。同样的可以像经典光线追踪一样，把这个像素点设定为黑色，或者背景颜色。在游戏场景中就是天空盒。
那么如果我们当前场景比较密闭呢，一条光线一直在场景中不断反射，就是没有击中光源的话，那怎么办？人为给定递归终止的条件：当光线碰撞了50次还没有击中光源或者射空（即递归50层），则终止递归，按照射空去处理。

光照模型：

Lambert 模型漫反射
Phong 模型同时考虑到了镜面反射都是单一光源情况
全局光照模型多光源更普适

向量

矩阵

光栅化