[OpenGL入门教程] 7. 使用GLM实现变换

注意 如果无法理解向量，矩阵以及变换的概念，请先了解下简单的线性代数，对其有所了解即可

OpenGL没有自带任何的矩阵和向量知识，但是我们可以使用已经做好了的数学库，专门为OpenGL量身定做的数学库，那就是GLM。

GLM是OpenGL Mathematics的缩写，它是一个只有头文件的库，只需包含对应的头文件就行了，不用链接和编译。GLM可以在它们的网站上下载。把头文件的根目录复制到你的includes文件夹，然后你就可以使用这个库了。

下载链接：https://github.com/g-truc/glm/releases/tag/0.9.8.5

测试GLM

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
// 译注：下面就是矩阵初始化的一个例子，如果使用的是0.9.9及以上版本
// 下面这行代码就需要改为:
// glm::mat4 trans = glm::mat4(1.0f)
// 之后将不再进行提示
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;

大多数需要的GLM的功能都可以从上面这3个头文件中找到

这里先用GLM内建的向量类定义一个叫做vec的向量作为将要被位移的向量，接下来定义一个mat4类型的trans，默认是一个4×4单位矩阵。

通过glm::translate可以创建转化矩阵，第一个参数传入单位矩阵，第二个参数传入位移的向量。这里，传入了一个(1.0,1.0,0.0)的位移。

最后把向量乘以位移矩阵并且输出最后的结果。

自己口算可以知道，结果应该是(2,1,0)。

对图形施加变化

glm::mat4 trans;
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));

unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));

首先，把图形在每个轴都缩放到0.5倍，然后沿z轴旋转90度。GLM希望它的角度是弧度制的(Radian)，所以要使用glm::radians将角度转化为弧度。

注意有纹理的那面矩形是在XY平面上的，所以需要把它绕着z轴旋转，即第三个参数。

因为我们把这个矩阵传递给了GLM的每个函数，GLM会自动将矩阵相乘，返回的结果是一个包括了多个变换的变换矩阵。

接着需要在主程序中添加一个uniform。首先查询uniform变量的地址，然后用有Matrix4fv后缀的glUniform函数把矩阵数据发送给着色器。

• 第一个参数是uniform的位置值。
• 第二个参数告诉OpenGL将要发送多少个矩阵，这里是1。
• 第三个参数询问我们是否希望对传入矩阵进行转置，也就是说交换矩阵的行和列。OpenGL开发者通常使用一种内部矩阵布局，叫做列主序布局。GLM的默认布局就是列主序，所以并不需要转置矩阵，填GL_FALSE。
• 最后一个参数是真正的矩阵数据，但是GLM并不是把它们的矩阵储存为OpenGL所希望接受的那种，因此要先用GLM的自带的函数value_ptr来变换这些数据。

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;

out vec2 TexCoord;

uniform mat4 transform;

void main()
{
    gl_Position = transform * vec4(aPos, 1.0f);
    TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
}

对应的，在shader代码中进行修改，引入转化矩阵，并将其左乘到坐标上。这样就可以完成一个缩放加旋转的变换了。

进一步，可以在循环之中创建随时间变换的变换矩阵，从而使得图形可以旋转起来。

glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));

最终应该出现如下情况：

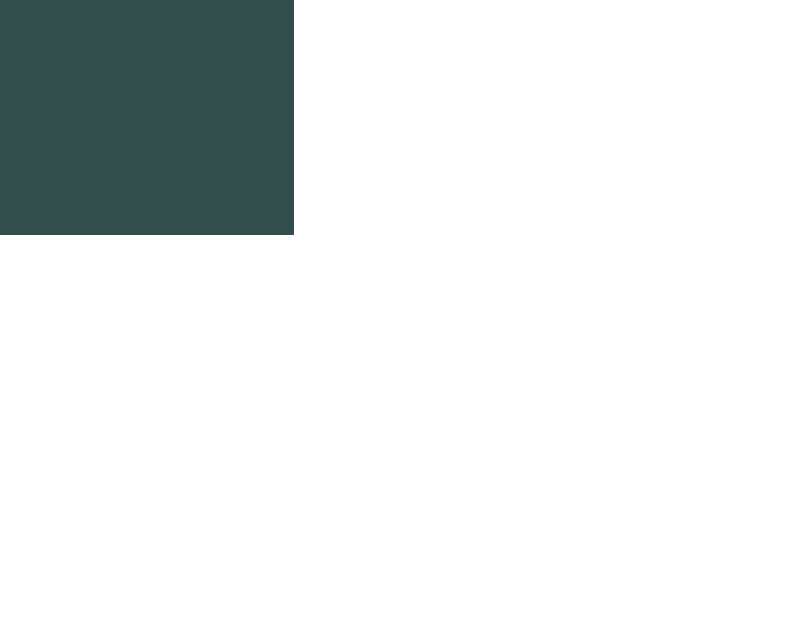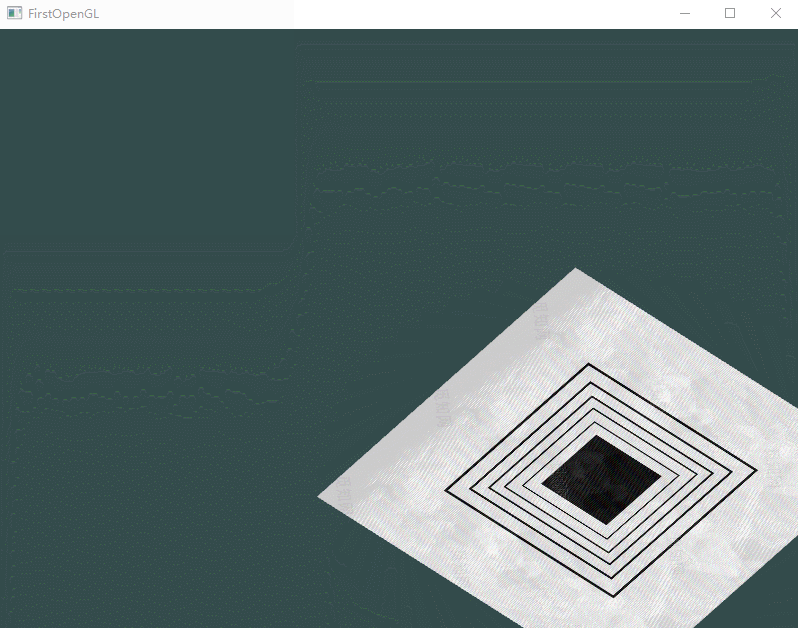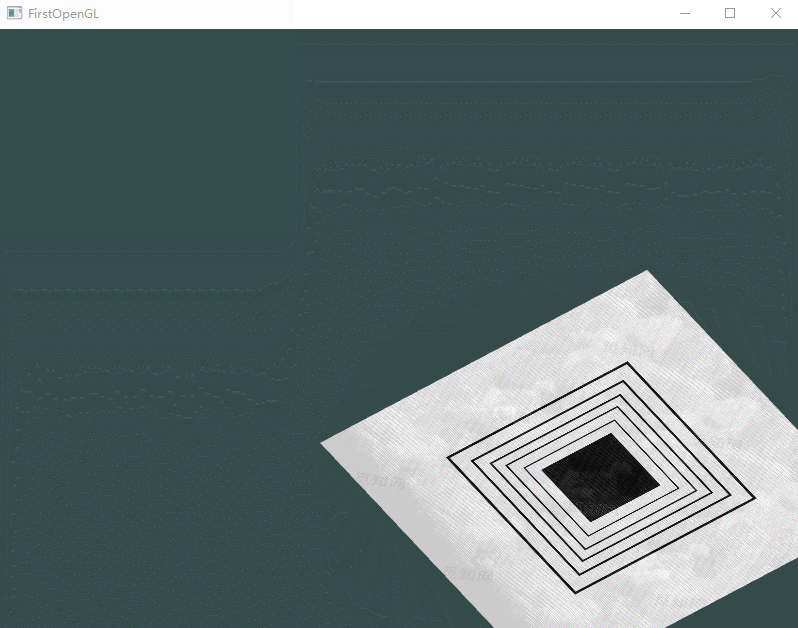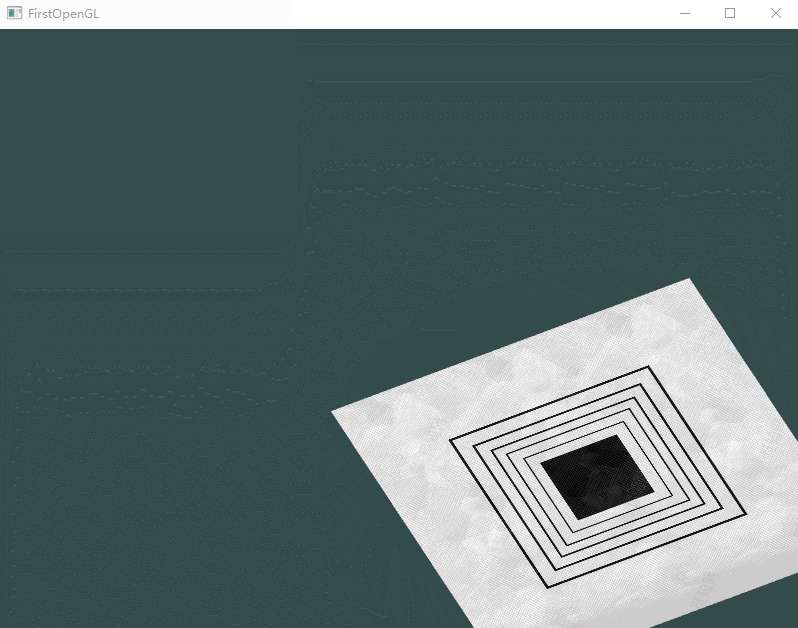
参考资料

[1] https://learnopengl-cn.readthedocs.io/zh/latest/01%20Getting%20started/03%20Hello%20Window/

[2] http://bit.ly/2lt7ccM