模型
用 public goods game (PGG) 公共物品博弈模型来表示人类能否达成合作
PGG:
N名玩家在不知道其他玩家选择的情况下,独立选择将初始资金的一部分投入公共池中。投入公共池的资金将被乘以一个系数作为“公共物品”,然后此“公共物品”将被平分给所有玩家。每位玩家还可获得初始资金中未
投入到公共池的部分。系数的范围为(1,N),即投入公共池会让资金带来更高的收益,但是不足以保证从公共物品中平分获得的收益一定大于原来的投入
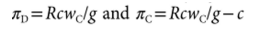
C表示合作者, D表示不合作者 其等价于一个连续的囚徒困境, 其纳什均衡是大家都不合作,最优解是都合作
在超图基础上,这篇文章提出了改进后的PGG模型:
- 首先以均匀概率随机选择超图中的节点
ni及其超边之一li。然后,对于任何一条选择的超边li, 超边的所有成员在他们所属的每个超边上都进行一轮博弈。 - 节点累积了他们玩的所有回合的收益,最后由其平均收益来表示。
- 节点
i将比较其收益与超边li中收益最大的节点的收益,,以一定概率采用超边中具有最大回报节点的策略
结果
无论在节点数均匀或异质,网络都呈现出临界效应——即只要超过特定值,网络中的合作者比例就会显著变化: 节点度数异质的网络(不同参数、不同节点度数分布)中,只要协作系数超过1,网络中合作者的比例就会迅速提升到100%
随着网络异质程度的增加,达到充分合作所需的协作系数降低,这意味着在合作者的人际网络具有多元化的环
境中,人们能够更容易地展开合作。