高阶相互作用: 超图和单纯复形
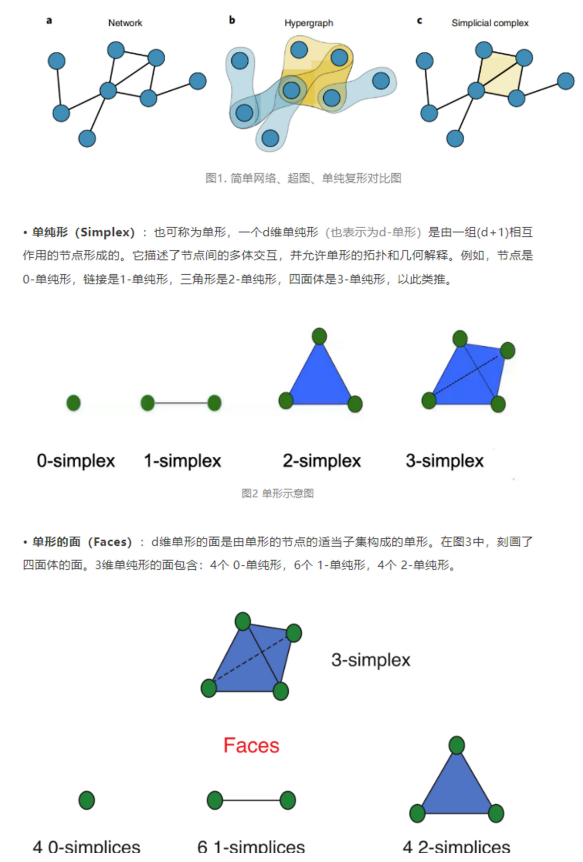

单纯复形骨架(Simplicial complex skeleton):d维单纯复形K中所有小于等于维度r的单纯形的集合,称为单纯复形K的r维骨架,记为Kr。如果只考虑一个单纯复形网络中的节点和连边,即为该单纯复形网络的1维骨架。
纯单纯复形(Pure simplicial complex):一个纯d维单纯复形是由一组d维单形及其面构成的。因此,纯d维单纯复形只允许d维单形作为面。这意味着纯d维单纯形复形是由d维单纯形沿着它们的表面粘接而形成的
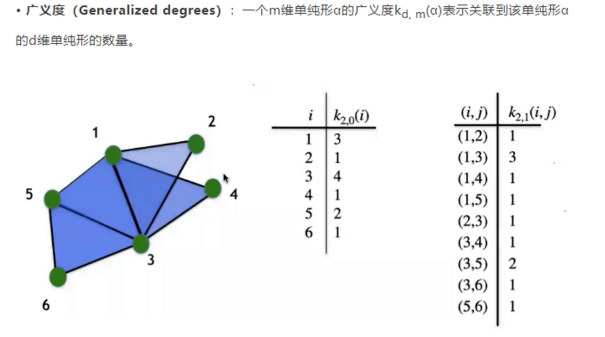
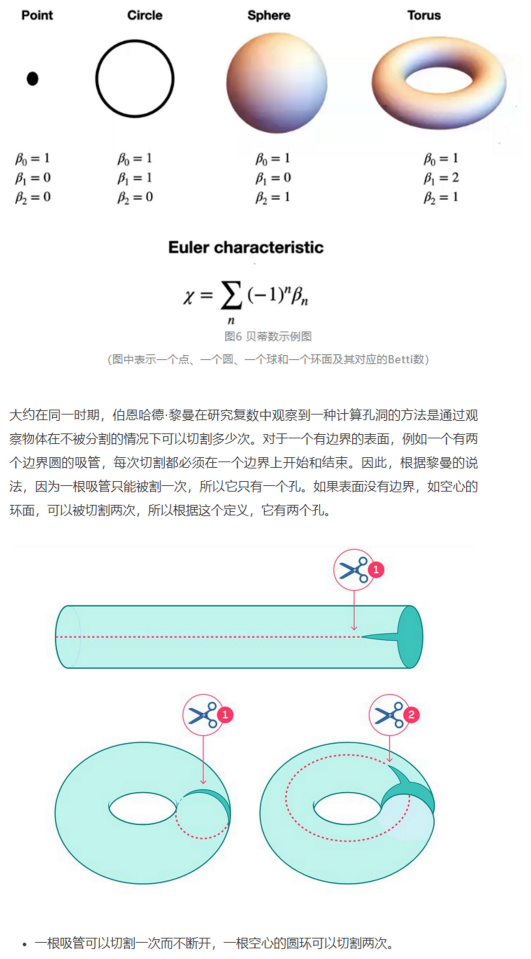
贝蒂数表示单纯复形的m维洞的数量,也等于同调群的秩。其中同调群是空间表示中的m-循环链的同调类,它
们与不是(m+1)-链边界的循环链有关
引入高阶互动
引入高阶互动后,能够用更细的粒度去描述系统中的非线性反馈
引入非线性的高阶相互作用并改变其强度,是促成爆发性转变的通用机制
高阶相互作用引入后能够探索的另一问题,即网络的拓扑结构如何随时间演化 同步现象会由高阶连接的部分扩散到低阶连接的部分(图b);或者相反,由低阶部分扩散到高阶部分
从观测数据中重构高阶相互作用网络
即使系统中存在高阶相互作用,但观察到的数据却往往是两两节点之间的。例如A从B处听到了一则谣言,但它可能是从B之前其他人那里传来的。如何根据时间序列推测高阶相互作用的存在呢?
通过贝叶斯推断或者统计模型中的零假设,用证据说明其存在,是重构高阶相互作用网络的两种常用方法。
除了直接观测到的相互影响事件,还可以通过系统的状态随时间的改变,来推断是否存在高阶相互作用,例如
节点间是否存在同步,是否有相关性等。
未来方向
当前的模型,都假设高阶相互作用出现与否不会随时间而改变。如何在模型中加入变化的高阶相互作用,是未
来的一个研究方向。